Простые математические формы и модели кристаллов

Не менее чем химический состав и геометрия структуры, интересны и важны для минералога и коллекционера природные внешние формы минералов. Знакомство с учением об этих формах - морфологией - переносит нас от абстрактного понятия минерального вида в мир конкретных минералов - тех самых, что мы находим в недрах Земли и видим в коллекциях.

   В природе минералы существуют в виде индивидов и их коллективов - агрегатов. Индивидом называется каждый отдельный кристалл независимо от его размеров и наличия правильных граней. Зерна полевого шпата, кварца и слюды, слагающие гранит, в такой же степени индивиды этих минералов, как и их красивые, симметричные кристаллы. В то же время искусственно ограненные куски минералов не являются индивидами, поскольку естественная форма в данном случае нарушена. Друзы и сростки кристаллов - наиболее интересные для коллекционера примеры минеральных агрегатов. Однако основная масса минералов образует сплошные массивные и зернистые агрегаты, в которых тесно сросшиеся индивиды чаще всего не имеют правильной и специфической для них формы. К таким агрегатам относятся, в частности, горные породы.

   Кристаллы. Отлагаясь в свободных пространствах, без помех со стороны других тел, минералы, как и все кристаллические тела, проявляют замечательное свойство самопроизвольно принимать правильную и индивидуальную для каждого минерального вида форму кристаллических многогранников. Это свойство - прямое следствие регулярности их внутреннего строения. На таких кристаллах следует остановиться подробно: как наиболее яркие представители мира минералов, они чрезвычайно интересны для науки и пользуются особой любовью коллекционеров. Но и в тех случаях, когда способность к самоогранению не реализована, минерал не перестает быть кристаллическим телом: достаточно того, что он имеет упорядоченное внутреннее строение.

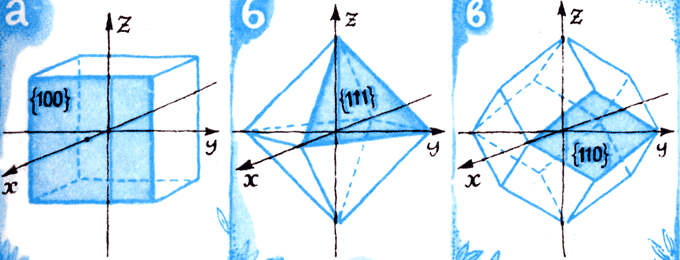
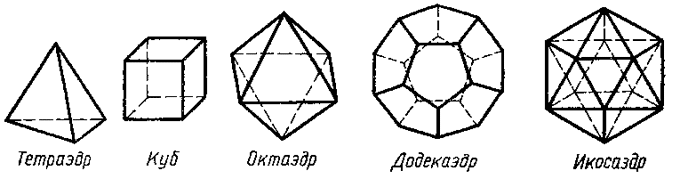
   "Кристаллы блещут симметрией" - так определил ее выдающийся кристаллограф Е.С.Федоров. Различия между формами кристаллов - это прежде всего различия в симметрии. На рисунке показаны главнейшие элементы симметрии, свойственные кристаллическим телам. Центр симметрии - точка внутри кристалла, обладающая следующим свойством: на любой проведенной через центр симметрии прямой на равных расстояниях от нее находятся соответствующие точки кристалла. Существует понятие центра симметрии: относительно него симметричны определенные вершины, грани и все другие точки кристалла. Ось симметрии - прямая, за один оборот вокруг которой кристалл дважды или несколько раз совмещается со своим начальным положением (по сути дела переходит сам в себя). Плоскость симметрии делит кристалл на две равные части, каждая из которых является зеркальным отражением другой. Других симметрий (более высокого порядка) в трехмерном пространстве не существует.

   "Самому скромному и простому, но и самому элегантному из камней - горному хрусталю, кварцу" (по выражению известного исследователя Г.Г.Леммлейна) суждено было долгое время служить главным объектом науки о кристаллах - кристаллографии. В 1669 г. датский геолог, физиолог и анатом Н.Стеной открыл, что кристаллы хрусталя растут посредством наслоения вещества и потому в процессе роста сохраняют неизменными углы между гранями. Стеной установил также закон постоянства углов, более чем столетие спустя сформулированный другим классиком кристаллографии, французом Ж. Б. Ромэ-Делилем: "Грани кристалла могут изменяться по своей форме и относительным размерам, но их взаимные наклоны постоянны и неизменны для каждого рода кристаллов". Как теперь известно, в основе этого закона лежит одинаковость структур всех кристаллов одного и того же вещества.

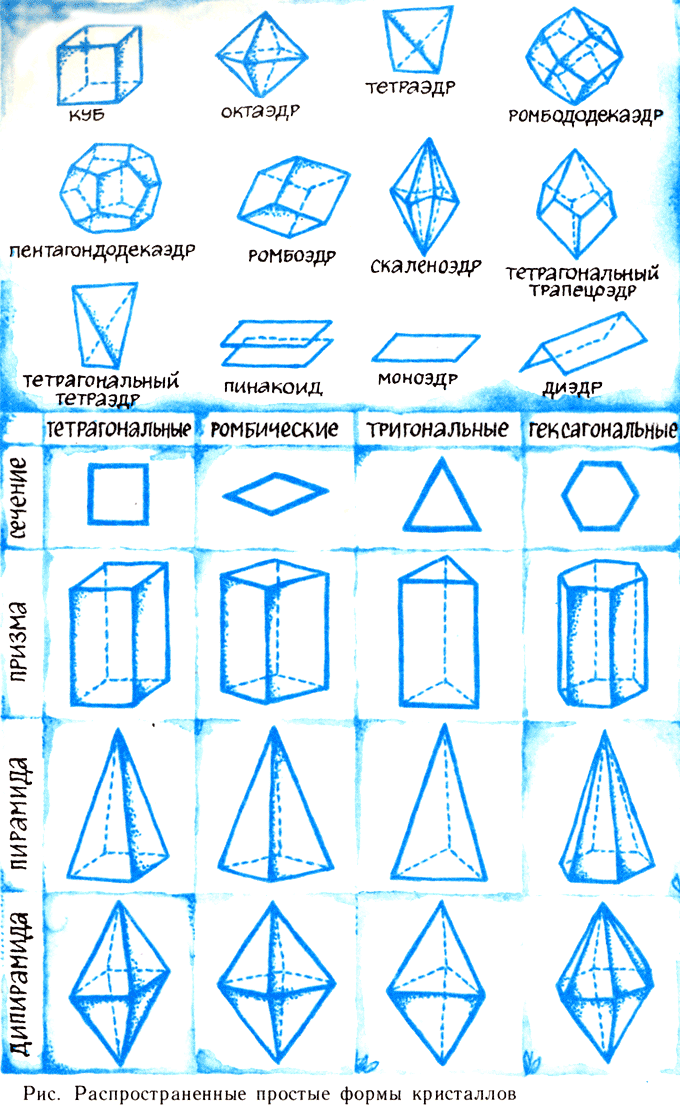
   Природное огранение каждого кристалла расчленяется на простые кристаллографические формы. В правильно образованных и целых кристаллах все грани одной простой формы одинаковы и связаны элементами симметрии. При образовании комбинации грани простых форм, пересекаясь, могут изменять свои очертания. Форму кристаллов определяют форму его кристаллической решетки.

   В мире минералов также широко распространены двойники и сростки. Эти агрегаты часто можно распознать по входящим углам у кристаллов. Существует ряд простых и сложных двойников. Так, у полевых шпатов карлсбадские двойники представляют собой простые двойники срастания, а манебахские двойники - это пример сложного двойникования. Другой формой двоиникования являются двойники прорастания, часто наблюдающиеся, например, у флюорита. Наряду с двойниками существуют также тройники и полисинтетические двойники. Кроме того, у ставролита, у авгита из базальтов и у ряда других минералов наблюдаются крестообразные двойники и сростания (у ставролита, например, под углами 60^o и 90^o).

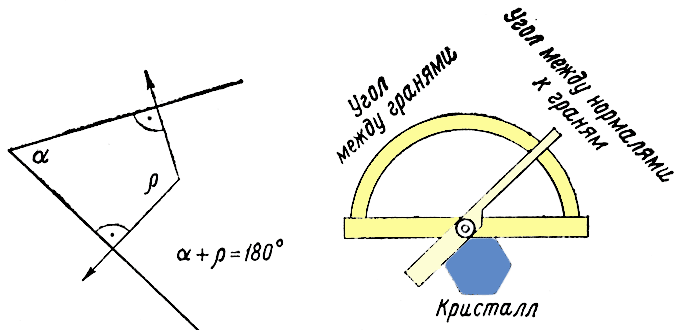
   В заключение следует познакомить любителей минералов с простым методом, который позволяет во многих случаях (в том числе в домашних условиях) точно диагностировать минералы по углам между гранями, но о котором в большинстве геологических определителей минералов не упоминается. В описаниях минералов наряду с сингонией приведены также класс симметрии и геометрическое осевое отношение, что облегчает возможность сравнения. Если минералы встречаются в искаженных формах, то сингония и тем более класс симметрии определяются с трудом. Однако это не мешает нам измерить углы между гранями кристалла.

   Искажение формы кристалла не затрагивает углов между кристаллографическими гранями. Углы между одинаковыми гранями кристалла всегда одинаковы. Углы между кристаллографическими гранями измеряются гониометром. Следует различать гранные углы и углы между нормалями (перпендикулярами) к граням. Первые дополняют вторые до 180^o (развернутого угла). С помощью простого прикладного угломера, который легко изготовить из транспортира и полоски картона, при аккуратной работе могут быть измерены углы с точностью до 1^o. Соответствующие грани минерала крепко зажимают между транспортиром и картонной линейкой и считывают значение угла между нормалями и гранями. Необходимо учитывать, что последующие вычисления действительны только для углов между нормалями (перпендикулярами) к граням.